Besaran Vektor & Skalar
Selamat Datang dan Selamat Belajar di Wardaya College! Kamu dapat download modul & kumpulan soal dalam bentuk pdf pada link dibawah ini:
Definisi
Pengertian vektor dan skalar, dalam fisika besaran dapat dikelompokkan berdasarkan komponen arahnya. Besaran Vektor adalah besaran yang memiliki nilai dan arah. Besaran Skalar adalah besaran yang tidak memiliki arah.
Besaran Vektor & Skalar
1. Besaran Vektor
Besaran vektor adalah besaran fisika yang memiliki nilai dan arah. Dalam hal ini nilai dan arah menjadi informasi yang saling melengkapi. Contoh besaran vektor adalah perpindahan, kecepatan, gaya, momentum, medan listrik dll.
Dalam menyatakan besaran vektor, nilai vektor harus diikuti dengan arahnya. Contoh kecepatan mobil 20 km/jam ke timur, mobil berpindah sejauh 400 meter ke kanan, Andi menarik mobil-mobilan dengan gaya 2 N ke kanan dll.
Serta penulisannya pun harus dibedakan dengan besaran bukan vektor. Biasanya dituliska dengan huruf cetak tebal, cetak miring atau huruf kapital. Contoh cara penulisan besaran vektor:
- Kecepatan disimbolkan dengan huruf vv
- Gaya disimbolkan dengan huruf FF
- Momentum disimbolkan dengan huruf pp
- dll
Besaran vektor digambarkan dengan anak panah lurus. Arah panah menunjukkan arah besarannya. Panjang garis anak panah merepresentasikan besar vektor.
Misalkan kita menggambarkan vektor kecepatan 2 m/s dengan garis 1 cm, maka untuk kecepatan sebesar 10 m/s harus digambarkan dengan garis sepanjang 5 cm dst. Berikut beberapa aturan berkaitan dengan rumus besaran vektor dan satuannya.
(a) Menggambar Besaran Vektor
Digambarkan dengan anak panah dengan panjang yang harus proporsional.
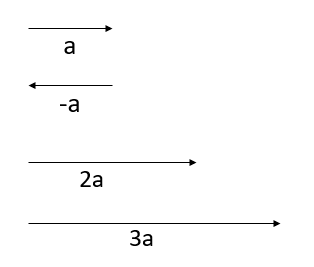
(b) Komponen Vektor dan Vektor Satuan
Suatu vektor dapat dinyatakan dalam bentuk komponen-komponennya. Misalkan sebuah vektor gaya FF membentuk sudut αα terhadap sumbu xx seperti gambar berikut.
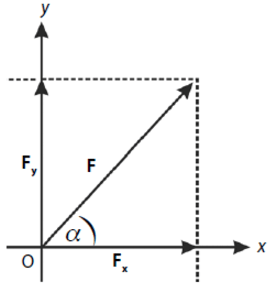
Vektor FF dapat diuraikan ke sumbu xx dan sumbu yy sebagai FxFx dan FyFy. FxFx dan FyFy disebut sebagai komponen vektor FF disumbu xx dan y.y. Besar komponen vektor di sumbu xx dan yy
adalah
Fx=F cos αFx=F cos α
Fy=F sin αFy=F sin α
Jika besar komponen vektor di sumbu xx adalah FxFx dan besar komponen vektor di sumbu yy adalah FyFy, maka vektor FF dapat dinyatakan dengan F=Fxi+Fyj,F=Fxi+Fyj, dengan ii dan jj adalah vektor satuan.
Vektor satuan (unit vektor) merupakan suatu vektor yang besarnya sama dengan 1 (satu) dan tidak mempunyai satuan serta berfungsi untuk menunjukan suatu arah dalam ruang.
Sebuah vektor yang terletak di dalam ruang tiga dimensi memiliki komponen-komponen terhadap sumbu x,x, sumbu yy dan sumbu zz, sehingga penulisannya harus menyertakan tiga vektor satuan i,j dan ki,j dan k. Misalkan vektor FF berada di ruang tiga dimensi maka vektor FF dapat dinyatakan sebagai F=Fxi+Fyj+Fzk.F=Fxi+Fyj+Fzk.
(c) Menjumlahkan dan Mengurangkan Vektor
Ada dua metode untuk menjumlahkan vektor, yaitu metode grafis (geometris) dan analisis. Metode grafis adalah penjumlahan vektor dengan menyatakan vektor-vektor dalam sebuah diagram. Panjang anak panah disesuaikan dengan besar vektor (artinya harus menggunakan skala dalam pengambarannya), dan arah vektor ditunjukkan oleh arah ujungnya (kepalanya).
Metode grafis dapat dilakukan dengan metode jajar genjang, segitiga dan metode poligon. Jika vektor AA,BB dan CC dengan besar tertentu maka penjumlahan dan pengurangan vektor secara grafis dapat digambarkan sebagai berikut.
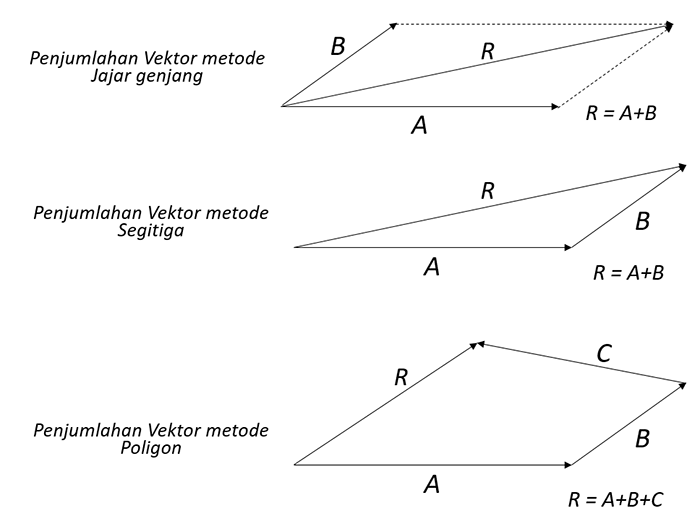
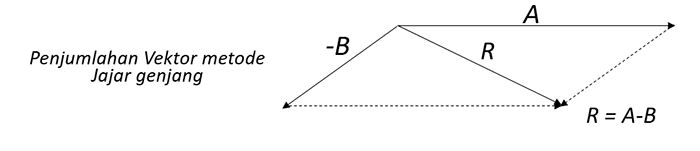
Penjumlahan dua vektor dalam dua dimensi, metoda geometris cukup memadai. Tetapi untuk kasus penjumlahan tiga vektor ataupun penjumlahan vektor dalam tiga dimensi seringkali kurang menguntungkan.
Cara lain yang dapat digunakan untuk menjumlahkan vektor adalah metoda analitik. Dengan metoda ini, vektor-vektor yang akan dijumlahkan, masing-masing diuraikan dalam komponen-komponen vektor arahnya (lihat kembali “Komponen Vektor”).
Pada intinya cara menjumlahkan vektor adalah sama dengan menjumlahkan bilangan bukan vektor. Perbedaannya adalah penjumlahan aljabar pada vektor hanya boleh dilakukan jika dua vektor tersebut adalah vektor yang memiliki dimensi yang sama dan bekerja pada sumbu yang sama . Vektor kecepatan tidak boleh dijumlahkan dengan vektor gaya, vektor gaya hanya boleh dijumlahkan dengan vektor gaya.
Misalkan vektor A dan B adalah vektor berdimensi sama dengan A=x1i+y1j+z1kA=x1i+y1j+z1k dan B=x2i+y2j+z2kB=x2i+y2j+z2k, maka A±B=(x1±x2)i+(y1±y2)j+(z1±z2)kA±B=(x1±x2)i+(y1±y2)j+(z1±z2)k.
Hasil penjumlahan ini masih dalam komponen-komponen vektor, untuk menentukan besar vektor hasil penjumlahan digunakan persamaan |A±B|=x2+y2+z2−−−−−−−−−−√|A±B|=x2+y2+z2 dengan x=x1±x2;x=x1±x2; y=y1±y2y=y1±y2 dan z=z1±z2.z=z1±z2.
(d) Perkalian Vektor
- Perkalian dengan konstanta
Jika A=x1i+y1j+z1kA=x1i+y1j+z1k maka b×A=bx1i+by1j+bz1kb×A=bx1i+by1j+bz1k. - Perkalian dengan vektor
- Perkalian dot
Perkalian dot adalah perkalian vektor yang menghasilkan besaran skalar, sehingga sering disebut sebagai “dot product”. Jika AA dan BB adalah vektor yang membentuk sudut θθ maka, A.B=AB cosθA.B=AB cosθ. - Perkalian cross
Jika AA dan BB adalah vektor yang membentuk sudut θθ maka, A×B=AB sinθA×B=AB sinθ. Hasil dari perkalian cross adalah vektor yang tegak lurus terhadap vektor-vektor yang dikalikan. Untuk lebih jelasnya bisa klik di link berikut (Video 1 dan 2).
- Perkalian dot
2. Besaran Skalar
Besaran yang memiliki besar, tetapi tidak memiliki arah disebut besaran skalar. Contohnya waktu, volume, massa jenis dan suhu.
Contoh Soal & Pembahasan
- Berikut ini yang termasuk besaran vektor adalah…..
- massa, waktu, panjang dan suhu
- jarak, kelajuan, kecepatan dan suhu
- perpindahan, kecepatan, gaya dan momentum
- momentum, energi, medan listrik dan jarak
- jarak, gaya magnet, energi dan daya
Jawaban: C
Besaran vektor adalah besaran yang memiliki nilai dan arah. Maka jawabannya adalah perpindahan, kecepatan, gaya dan momentum.
- Besar gaya Lorentz dari muatan sebesar qq yang bergerak di medan magnet BB dengan kecepatan vv adalah sebesar F=q(v×B)F=q(v×B). Jika partikel bermuatan 22 mC bergerak di medan B=2i+5jB=2i+5j T dengan kecepatan v=5iv=5i m/s, maka besar dan arah gaya Lorentznya adalah….
- 35k35k mN
- 50k50k mN
- 70k70k mN
- 80k80k mN
- 90k90k mN
Jawaban: B
Berdasarkan persamaan di gaya lorentz maka
F=q(v×B)=2×10−3(5i×(2i+5j))=50×10−3kN=50k mNF=q(v×B)=2×10−3(5i×(2i+5j))=50×10−3kN=50k mN
- Vektor A memiliki besar A=2i+5j+2kA=2i+5j+2k dan vektor B memiliki besar B=4i+bi+1kB=4i+bi+1k, jika A⋅B=A⋅B=20, maka besar bb adalah….
- 1
- 2
- 3
- 4
- 5
Jawaban: B
A⋅B2010b=(2i+5j+2k)⋅(4i+bi+1k)=8+5b+2=5b=2A⋅B=(2i+5j+2k)⋅(4i+bi+1k)20=8+5b+210=5bb=2
Latihan Soal Besaran Vektor & Skalar (Mudah)
-
Pertanyaan ke 1 dari 5
Vektor perpindahan VV memiliki komponen horisontal sebesar 21 m seperti gambar berikut.
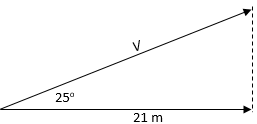
Komponen vertikal vektor tersebut mendekati nilai…
- 8 m
- 10 m
- 12 m
- 14 m
- 16 m
Betul
V=Vxtanθ=21×tan25=9,79 mV=Vxtanθ=21×tan25=9,79 m
Dibulatkan menjasi 10 m.
Latihan Soal Besaran Vektor & Skalar (Sedang)
-
Pertanyaan ke 1 dari 5
Vektor kecepatan pada gerak dengan percepatan konstan dapat ditentukkan dengan persamaan v=v0−atv=v0−at. Berdasarkan persamaan tersebut maka….
- Arah vektor kecepatan vv berlawanan dengan arah vektor percepatan v0v0.
- Arah vektor kecepatan vv berlawanan dengan arah vektor percepatan aa.
- Arah vektor kecepatan vv berlawanan dengan arah vektor percepatan tt.
- Arah vektor kecepatan vv berlawanan dengan arah vektor percepatan −t−t.
- Arah vektor kecepatan vv berlawanan dengan arah vektor percepatan −a−a.
Latihan Soal Besaran Vektor & Skalar (Sukar)
-
Pertanyaan ke 1 dari 5
Resultan gaya pada arah vertikal FF yang bekerja pada sebuah balon digambarkan sebagai berikut. Akibat terkena tiupan angin AA, tali pengikat balon menyimpang sejauh θθ terhadap vertikal.
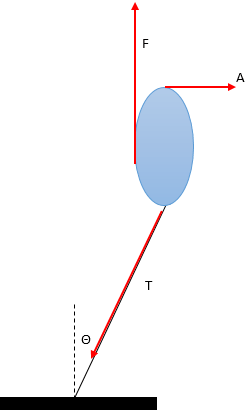
Hubungan antara tegangan tali TT dan gaya angin AA dengan FF adalah….
- T=F cosθT=F cosθ dan A=FsinθA=Fsinθ
- T=FsinθT=Fsinθ dan A=FcosθA=Fcosθ
- T=FcosθT=Fcosθ dan A=FsinθA=Fsinθ
- T=FsinθT=Fsinθ dan A=F cosθA=F cosθ
- T=FtanθT=Ftanθ dan A=Fcosθ








